An object-oriented design to tackle general TSPs as a bedrock for modeling more complex routing problemsPhoto by Kelsey Knight on Unsplash?? This is article #5 of the series covering the project “An Intelligent Decision Support System for Tourism in Python”. I...

An object-oriented design to tackle general TSPs as a bedrock for modeling more complex routing problems

Photo by Kelsey Knight on Unsplash?? This is article #5 of the series covering the project “An Intelligent Decision Support System for Tourism in Python”. I encourage you to check it out to get a general overview of the whole project. If you’re only interested in solving TSPs, this article is still for you, as I show an approach that makes it incredibly simple to solve any TSP. The article does build upon the previous ones, but reading them is optional; do so if you’d like to know the “how”, or skip them if you want to just have something working as soon as possible.

In sprint 5, we’ll design an optimizer class that, by hiding away all the low-level modeling details, allows us to seamlessly solve TSP problems. If you feel the present article lacks enough context or makes big jumps, please read the “prep work” for it: how to implement a model for the TSP in Pyomo, and how to find distances between locations in an automatic manner.

Table of contents

1. Previous sprints recap

2. Read data for the sites to be visited

3. The basic architecture

3.1. The Optimizer class diagram3.2. GeoAnalyzer, revisited3.3. Laying the bases: a base class for optimization utilities

4. One class to route them all: the TravelingSalesmanOptimizer

4.1. TravelingSalesmanOptimizer design4.2. TravelingSalesmanOptimizer implementation4.2. TravelingSalesmanOptimizer for dummies

5. Beyond the optimal solution: extracting insights with the optimizer

6. Conclusion (or planning for next sprint)

1. Previous sprints recap

In sprint 1 we reasoned our way through a ubiquitous tourism planning problem and concluded that its minimum valuable problem took the form of the Traveling Salesman Problem (TSP). That is why we dedicated sprint 2 and sprint 3 to develop a mathematical model, and a computer model, respectively, of the TSP. However, the goal then was only to demonstrate the viability of using optimization modeling to solve such a problem. Once this proof-of-concept was deemed viable, the new goal was to upgrade it, to refine it into a Minimum Viable Product (MVP) that could be used to solve this kind of problems systematically, and in a more general fashion. We noticed that, as a prerequisite, we needed a way of obtaining distance data from arbitrary locations. We tackled this issue in sprint 4, where we built the GeoAnalyzer class to compute the distance matrix for any set of locations given only their coordinates.

All those iterative advancements take us here, to sprint 5, where we finally hit a major milestone: the creation of an estimator-like class that solves general TSPs, quickly and intuitively. We will accomplish this by integrating what we’ve built so far in an extensible fashion, thereby paving the way for future enhancements that will extend the capabilities of our model far beyond the TSP, something we must do if our system is to solve realistic tourism problems.

That said, the Traveling Salesman Problem?—?arguably the most famous transportation problem in all Operations Research?—?is in a class of its own, so in this article, we’ll give it a class of its own.

2. Read data for the sites to be visited

The basic input for the generic TSP is the locations we want to visit. In our example, we have a list of sites of interest in Paris, including our hotel. Let’s read them into a dataframe:

import pandas as pd


def read_data_sites_to_visit() -> pd.DataFrame:
""" Reads in a dataframe the locations of the sites to visit """
DATA_FOLDER = ("https://raw.githubusercontent.com/carlosjuribe/"
"traveling-tourist-problem/main/data")
FILE_LOCATION_HOTEL = "location_hotel.csv"
FILE_LOCATION_SITES = "sites_coordinates.csv"

df_sites = pd.concat([
# coordinates of our hotel, the starting location
pd.read_csv(f"{DATA_FOLDER}/{FILE_LOCATION_HOTEL}", index_col='site'),
# coordinates of the actual places we want to visit
pd.read_csv(f"{DATA_FOLDER}/{FILE_LOCATION_SITES}", index_col='site'),
])
return df_sites

df_sites = read_data_sites_to_visit()

df_sites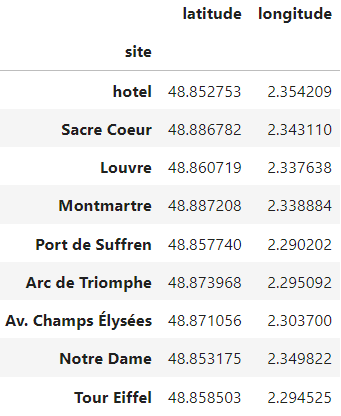Figure 1. Input coordinates for the optimizer (Image by author)

3. The basic architecture

Before we start coding, it’s important to have a high-level understanding, and thus a design, of what we are about to do and why. Our goal is the creation of a class that takes in some geographical coordinates of some sites, and solves the TSP problem for them, i.e., outputs the order in which we ought to visit those sites to minimize the total distance traveled. We won’t create just one class that does everything; we will keep different functionalities in different classes, and then combine them together¹.

3.1. The Optimizer class diagram

I believe it is convenient for our class to have a scikit-learn-ish API. However, I won’t refer to our new class as an “estimator”, but rather, as an “optimizer”². A self-explanatory name is TravelingSalesmanOptimizer. One of its helper attributes will be the GeoAnalyzer class built in sprint 4. Also, as this won't be the only optimizer class we'll end up creating in this project, we will store all the functionality related to the solving of models inside a separate class, BaseOptimizer. The reason is that all optimizers, no matter what internal model they implement, will need to optimize it, so it's best to keep the logic related to the optimization itself in a separate class, a base class which all optimizers will inherit from.

In the class diagram below, we can see how the three classes fit together. Inside each, I have included their main attributes and methods (but not all) for us to get the idea.

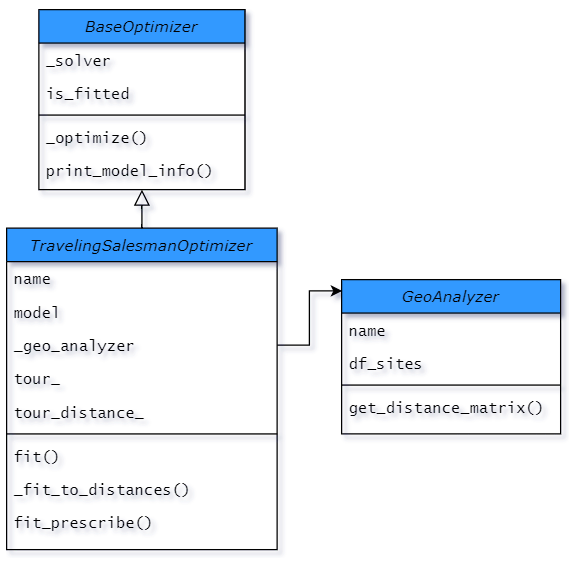Figure 2. Class diagram for the TSP Optimizer (Image by author)

Here’s the main purpose of each class, in a nutshell:

BaseOptimizer is responsible for the optimization of the models of "proper" optimizer subclasses, it's not intended to be instantiated on its own.GeoAnalyzer is a self-contained class of geo-utilities. It aids in the crucial step of computing a distance matrix from user-given coordinates, needed to construct a model if the user doesn't have custom distance data at hand.The TravelingSalesmanOptimizer is an optimizer that can be fitted to a dataframe having the coordinates of the sites. Once fitted, the "visit order" of those sites can be retrieved. Internally, it implements a mathematical model of the Traveling Salesman Problem as a Pyomo model object.

With a concrete design in mind, let’s assemble it.

3.2. GeoAnalyzer, revisited

As the code for GeoAnalyzer was already developed in the previous sprint, here we just move it to a new module, geoutils.py, and import the class from there. If you haven't read the article in which it was created, don't worry, all you need to know is that it takes in some dataframe of coordinates and outputs a distance matrix, like this:

from geoutils import GeoAnalyzer

geo_analyzer = GeoAnalyzer()
geo_analyzer.add_locations(df_sites)
df_distances = geo_analyzer.get_distance_matrix(precision=0)

display(df_distances)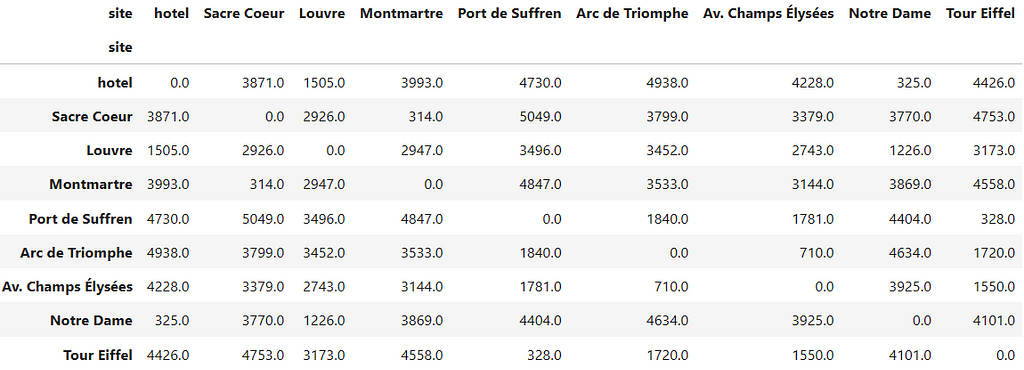Figure 3. Distance matrix generated by GeoAnalyzer (Image by author)

This dataframe of distances is what we’ll use inside TravelingSalesmanOptimizer to create an internal model, as the real data that is needed to model a Traveling Salesman problem is distances, not coordinates.

3.3. Laying the bases: a base class for optimization utilities

In the article for sprint 3, the very first code snippet is about instantiating a Pyomo solver and printing its version. A bit further below, in section 2.1, we used this solver to optimize the model. With that in mind, creating BaseOptimizer is only a matter of putting these pieces together into a class. We will modify the original code slightly so that it becomes easier to read, but essentially it's the same thing wrapped conveniently.

import sys

import pyomo.environ as pyo


class BaseOptimizer:
""" Base class for common functionality shared among optimizers,
regarding generic handling and solving of optimization models.
It's not intended to be used by itself but as an abstract class
to be extended by actual optimizers that implement concrete Pyomo models.

Attributes
----------
_solution_exists : bool (default=None)
Initially None, it takes a boolean value after a (subclass) optimizer
has had a fitting attempt: True if an optimal solution was found, False
otherwise. If the value is None, it means the optimizer hasn't been fit
to any data yet.

is_fitted : bool
True if-and-only-if the optimizer has been fitted successfully
and thus an optimal solution was found.
"""
def __init__(self):
self._solution_exists = None # updated to True/False inside `_optimize`
self._setup_solver()

####################### solver setup #######################
def _setup_solver(self, solver_nickname="glpk"):
""" Instantiates and stores a MILP solver as an internal attribute """
solver = pyo.SolverFactory(solver_nickname)
if not solver.available(exception_flag=False):
raise Exception(f"Solver '{solver_nickname}' not found. "
"You can install it by running:\n"
"conda install -y -c conda-forge glpk")
self._solver = solver

def _print_solver_info(self) -> None:
print("Solver info:",
f"name: {self._solver.name}",
f"version: {self._solver.version()}",
sep="\n - ")

###################### model handling ######################
def _optimize(self, model: pyo.ConcreteModel) -> bool:
""" Solve the model. If an optimal solution is found, the model
provided will have the solution inside and ?True? is returned.
If an optimal solution isn't found, a warning is printed, the
results of the optimization are stored in the ?_results? attribute
(so post-mortem analysis can be done) and False is returned """
res = self._solver.solve(model)
self._results = res # store output of solver for inspection
self._solution_exists = pyo.check_optimal_termination(res)

# _solution_exists is True iff an optimal solution is found
if not self._solution_exists:
print("Optimal solution not found, check attribute '_results' "
"for details", file=sys.stderr)
return self._solution_exists

def _store_model(self, model: pyo.ConcreteModel) -> None:
""" Stores the Pyomo model as a public attribute """
self.model = model

@property
def is_model_created(self) -> bool:
""" True if the (sub)class has an attribute named `model` """
return hasattr(self, 'model')

@property
def is_fitted(self) -> bool:
""" Returns whether the model of the child class has been fitted
(i.e., solved) successfully. Returns False otherwise, i.e.,
if model hasn't been optimized yet, or if an optimal solution
wasn't found """
return bool(self._solution_exists)

######################## model inspection ########################
def print_model_info(self) -> None:
""" High-level overview of the number of components
(i.e., constraints, variables, etc.) in the model """
if not self.is_model_created:
print("No internal model exists yet. Fit me to some data first")
return

print(f"Name: {self.model.name}",
f"Num variables: {self.model.nvariables()}",
f"Num constraints: {self.model.nconstraints()}",
f"Num objectives: {self.model.nobjectives()}",
sep="\n- ")

The main things to keep in mind about this class are:

At instantiation, the solver is set up internally by _setup_solver. As we can't solve any model without a solver, if the setup fails, an exception will be raised. If the solver is found, it's kept as a private attribute.The method _optimize will be invoked whenever a subclass to BaseOptimizer calls a fit-like method. _optimize takes in a model and attempts to solve it, using the internal solver. If an optimal solution exists, the attribute _solution_exists will cease to be None and will take the value True. If no optimal solution exists³, it will take the value False, and a warning is printed.

The remaining methods are explained in their docstrings. Now, time to build our first optimizer.

4. One class to route them all: the TravelingSalesmanOptimizer

Here we won’t start from scratch. As stated earlier, we already developed the code that builds a Pyomo model of the TSP and solves it in sprint 3. And trust me, that was the hardest part. Now, we have the easier task of organizing what we did in a way that makes it general, hiding the details while keeping the essential elements visible. In a sense, we want the optimizer to look like a “magic box” that even users not familiar with math modeling are able to use to solve their TSP problems intuitively.

4.1. TravelingSalesmanOptimizer design

Our optimizer class will have “core” methods, doing the bulk of the work, and “superficial” methods, serving as the high-level interface of the class, which invoke the core methods underneath.

These are the steps that will lie at the core of the optimizer’s logic:

Create a Pyomo model out of a distance matrix. This is done by the _create_model method, which basically wraps the code of the proof-of-concept we already did. It accepts a dataframe of a distance matrix and builds a Pyomo model out of it. The only important difference between what we did and what we're doing is that, now, the initial site is not hard-coded as simply "hotel", but is assumed to be the site of the first row in df_distances. In the general case, thus, the initial site is taken to be the first one in the coordinates dataframe? df_sites. This generalization allows the optimizer to solve any instance.(Attempt to) Solve the model. This is performed in the _optimize method inherited from BaseOptimizer, which returns True only if a solution is found.Extract the solution from the model and parse it in a way that is easy to interpret and use. This happens inside _store_solution_from_model, which is a method that inspects the solved model and extracts the values of the decision variables, and the value of the objective function, to create the attributes tour_ and tour_distance_, respectively. This method gets invoked only if a solution exists, so if no solution is found, the "solution attributes" tour_ and tour_distance_ never get created. The benefit of this is that the presence of these two "solution attributes", after fitting, will inform the user of the existence of a solution. As a plus, the optimal values of both the variables and objective can be conveniently retrieved at any point, not necessarily at the moment of fitting.

The last 2 steps?—?finding and extracting the solution?—?are wrapped inside the last “core” method, _fit_to_distances.

“But wait”?—?you might think?—?“As the name implies, _fit_to_distances requires distances as input; isn't our goal to solve TSP problems using only coordinates, not distances?". Yes, that's where the fit method fits in. We pass coordinates to it, and we take advantage of GeoAnalyzer to construct the distance matrix, which is then processed normally by _fit_to_distances. In this way, if the user does not want to collect the distances himself, he can delegate the task by using fit. If, however, he prefers to use custom data, he can assemble it in a df_distances and pass it to _fit_to_distances instead.

4.2. TravelingSalesmanOptimizer implementation

Let’s follow the design outlined above to incrementally build the optimizer. First, a minimalist version that just builds a model and solves it?—?without any solution parsing yet. Notice how the __repr__ method allows us to know the name and number of sites the optimizer contains whenever we print it.

from typing import Tuple, List


class TravelingSalesmanOptimizer(BaseOptimizer):
"""Implements the Miller–Tucker–Zemlin formulation [1] of the
Traveling Salesman Problem (TSP) as a linear integer program.
The TSP can be stated like: "Given a set of locations (and usually
their pair-wise distances), find the tour of minimal distance that
traverses all of them exactly once and ends at the same location
it started from. For a derivation of the mathematical model, see [2].

Parameters
----------
name : str
Optional name to give to a particular TSP instance

Attributes
----------
tour_ : list
List of locations sorted in visit order, obtained after fitting.
To avoid duplicity, the last site in the list is not the initial
one, but the last one before closing the tour.

tour_distance_ : float
Total distance of the optimal tour, obtained after fitting.

Example
--------
>>> tsp = TravelingSalesmanOptimizer()
>>> tsp.fit(df_sites) # fit to a dataframe of geo-coordinates
>>> tsp.tour_ # list ofsites sorted by visit order

References
----------
[1] https://en.wikipedia.org/wiki/Travelling_salesman_problem
[2] https://towardsdatascience.com/plan-optimal-trips-automatically-with-python-and-operations-research-models-part-2-fc7ee8198b6c
"""
def __init__(self, name=""):
super().__init__()
self.name = name

def _create_model(self, df_distances: pd.DataFrame) -> pyo.ConcreteModel:
""" Given a pandas dataframe of a distance matrix, create a Pyomo model
of the TSP and populate it with that distance data """
model = pyo.ConcreteModel(self.name)

# a site has to be picked as the "initial" one, doesn't matter which
# really; by lack of better criteria, take first site in dataframe
# as the initial one
model.initial_site = df_distances.iloc[0].name

#=========== sets declaration ===========#
list_of_sites = df_distances.index.tolist()

model.sites = pyo.Set(initialize=list_of_sites,
domain=pyo.Any,
doc="set of all sites to be visited (?)")

def _rule_domain_arcs(model, i, j):
""" All possible arcs connecting the sites (?) """
# only create pair (i, j) if site i and site j are different
return (i, j) if i != j else None

rule = _rule_domain_arcs
model.valid_arcs = pyo.Set(
initialize=model.sites * model.sites, # ? × ?
filter=rule, doc=rule.__doc__)

model.sites_except_initial = pyo.Set(
initialize=model.sites - {model.initial_site},
domain=model.sites,
doc="All sites except the initial site"
)
#=========== parameters declaration ===========#
def _rule_distance_between_sites(model, i, j):
""" Distance between site i and site j (???) """
return df_distances.at[i, j] # fetch the distance from dataframe

rule = _rule_distance_between_sites
model.distance_ij = pyo.Param(model.valid_arcs,
initialize=rule,
doc=rule.__doc__)

model.M = pyo.Param(initialize=1 - len(model.sites_except_initial),
doc="big M to make some constraints redundant")

#=========== variables declaration ===========#
model.delta_ij = pyo.Var(model.valid_arcs, within=pyo.Binary,
doc="Whether to go from site i to site j (???)")

model.rank_i = pyo.Var(model.sites_except_initial,
within=pyo.NonNegativeReals,
bounds=(1, len(model.sites_except_initial)),
doc=("Rank of each site to track visit order"))

#=========== objective declaration ===========#
def _rule_total_distance_traveled(model):
""" total distance traveled """
return pyo.summation(model.distance_ij, model.delta_ij)

rule = _rule_total_distance_traveled
model.objective = pyo.Objective(rule=rule,
sense=pyo.minimize,
doc=rule.__doc__)

#=========== constraints declaration ===========#
def _rule_site_is_entered_once(model, j):
""" each site j must be visited from exactly one other site """
return sum(model.delta_ij[i, j]
for i in model.sites if i != j) == 1

rule = _rule_site_is_entered_once
model.constr_each_site_is_entered_once = pyo.Constraint(
model.sites,
rule=rule,
doc=rule.__doc__)

def _rule_site_is_exited_once(model, i):
""" each site i must departure to exactly one other site """
return sum(model.delta_ij[i, j]
for j in model.sites if j != i) == 1

rule = _rule_site_is_exited_once
model.constr_each_site_is_exited_once = pyo.Constraint(
model.sites,
rule=rule,
doc=rule.__doc__)

def _rule_path_is_single_tour(model, i, j):
""" For each pair of non-initial sites (i, j),
if site j is visited from site i, the rank of j must be
strictly greater than the rank of i.
"""
if i == j: # if sites coincide, skip creating a constraint
return pyo.Constraint.Skip

r_i = model.rank_i[i]
r_j = model.rank_i[j]
delta_ij = model.delta_ij[i, j]
return r_j >= r_i + delta_ij + (1 - delta_ij) * model.M

# cross product of non-initial sites, to index the constraint
non_initial_site_pairs = (
model.sites_except_initial * model.sites_except_initial)

rule = _rule_path_is_single_tour
model.constr_path_is_single_tour = pyo.Constraint(
non_initial_site_pairs,
rule=rule,
doc=rule.__doc__)

self._store_model(model) # method inherited from BaseOptimizer
return model

def _fit_to_distances(self, df_distances: pd.DataFrame) -> None:
self._name_index = df_distances.index.name
model = self._create_model(df_distances)
solution_exists = self._optimize(model)
return self

@property
def sites(self) -> Tuple[str]:
""" Return tuple of site names the optimizer considers """
return self.model.sites.data() if self.is_model_created else ()

@property
def num_sites(self) -> int:
""" Number of locations to visit """
return len(self.sites)

@property
def initial_site(self):
return self.model.initial_site if self.is_fitted else None

def __repr__(self) -> str:
name = f"{self.name}, " if self.name else ''
return f"{self.__class__.__name__}({name}n={self.num_sites})"

Let’s quickly check how the optimizer behaves. Upon instantiation, the optimizer does not contain any number of sites, as the representation string shows, or an internal model, and it’s of course not fitted:

tsp = TravelingSalesmanOptimizer("trial 1")

print(tsp)
#[Out]: TravelingSalesmanOptimizer(trial 1, n=0)
print(tsp.is_model_created, tsp.is_fitted)
#[Out]: (False, False)

We now fit it to the distance data, and if we don’t get a warning, it means that it all went well. We can see that now the representation string tells us we provided 9 sites, there’s an internal model, and that the optimizer was fitted to the distance data:

tsp._fit_to_distances(df_distances)

print(tsp)
#[Out]: TravelingSalesmanOptimizer(trial 1, n=9)
print(tsp.is_model_created, tsp.is_fitted)
#[Out]: (True, True)

That the optimal solution was found is corroborated by the presence of definite values in the rank decision variables of the model:

tsp.model.rank_i.get_values(){'Sacre Coeur': 8.0,
'Louvre': 2.0,
'Montmartre': 7.0,
'Port de Suffren': 4.0,
'Arc de Triomphe': 5.0,
'Av. Champs Élysées': 6.0,
'Notre Dame': 1.0,
'Tour Eiffel': 3.0}

These rank variables represent the chronological order of the stops in the optimal tour. If you recall from their definition, they are defined over all sites except the initial one?, and that’s why the hotel does not appear in them. Easy, we could add the hotel with rank 0, and there we would have the answer to our problem. We don’t need to extract ???, the decision variables for the individual arcs of the tour, to know in which order we should visit the sites. Although that’s true, we’re still going to use the arc variables ??? to extract the exact sequence of stops from the solved model.

? Agile doesn’t need to be fragileIf our only aim were to solve the TSP, without looking to extend the model to encompass more details of our real-life problem, it would be enough to use the rank variables to extract the optimal tour. However, as the TSP is just the initial prototype of what will become a more sophisticated model, we’re better off extracting the solution from the arc decision variables ???, as they will be present in any model that involves routing decisions. All other decision variables are auxiliary, and, when needed, their job is to represent states or indicate conditions dependant on the true decision variables, ???. As you’ll see in the next articles, choosing the rank variables to extract the tour works for a pure TSP model, but won’t work for extensions of it that make it optional to visit some sites. Hence, if we extract the solution from ???, our approach will be general and re-usable, no matter how complex the model we’re using.

The benefits of this approach will become apparent in the following articles, where new requirements are added, and thus additional variables are needed inside the model. With the why covered, let’s jump into the how.

4.2.1 Extracting the optimal tour from the model

We have the variable ???, indexed by possible arcs (i, j), where ???=0 means the arc is not selected and ???=1 means the arc is selected.We want a dataframe where the sites are in the index (as in our input df_sites), and where the stop number is indicated in the column "visit_order".We write a method to extract such dataframe from the fitted optimizer. These are the steps we’ll follow, with each step encapsulated in its own helper method(s):Extract the selected arcs from ???, which represents the tour. Done in _get_selected_arcs_from_model.Convert the list of arcs (edges) into a list of stops (nodes). Done in _get_stops_order_list.Convert the list of stops into a dataframe with a consistent structure. Done in _get_tour_stops_dataframe.

As the selected arcs are mixed (i.e., not in “traversing order”), getting a list of ordered stops is not that straight-forward. To avoid convoluted code, we exploit the fact that the arcs represent a graph, and we use the graph object G_tour to traverse the tour nodes in order, arriving at the list easily.

import networkx as nx


# class TravelingSalesmanOptimizer(BaseOptimizer):
# def __init__()
# def _create_model()
# def _fit_to_distances()
# def sites()
# def num_sites()
# def initial_site()

_Arc = Tuple[str, str]

def _get_selected_arcs_from_model(self, model: pyo.ConcreteModel) -> List[_Arc]:
"""Return the optimal arcs from the decision variable delta_{ij}
as an unordered list of arcs. Assumes the model has been solved"""
selected_arcs = [arc
for arc, selected in model.delta_ij.get_values().items()
if selected]
return selected_arcs

def _extract_solution_as_graph(self, model: pyo.ConcreteModel) -> nx.Graph:
"""Extracts the selected arcs from the decision variables of the model, stores
them in a networkX graph and returns such a graph"""
selected_arcs = self._get_selected_arcs_from_model(model)
self._G_tour = nx.DiGraph(name=model.name)
self._G_tour.add_edges_from(selected_arcs)
return self._G_tour

def _get_stops_order_list(self) -> List[str]:
"""Return the stops of the tour in a list **ordered** by visit order"""
visit_order = []
next_stop = self.initial_site # by convention...
visit_order.append(next_stop) # ...tour starts at initial site

G_tour = self._extract_solution_as_graph(self.model)
# starting at first stop, traverse the directed graph one arc at a time
for _ in G_tour.nodes:
# get consecutive stop and store it
next_stop = list(G_tour[next_stop])[0]
visit_order.append(next_stop)
# discard last stop in list, as it's repeated (the initial site)
return visit_order[:-1]

def get_tour_stops_dataframe(self) -> pd.DataFrame:
"""Return a dataframe of the stops along the optimal tour"""
if self.is_fitted:
ordered_stops = self._get_stops_order_list()
df_stops = (pd.DataFrame(ordered_stops, columns=[self._name_index])
.reset_index(names='visit_order') # from 0 to N
.set_index(self._name_index) # keep index consistent
)
return df_stops

print("No solution found. Fit me to some data and try again")

Let’s see what this new method gives us:

tsp = TravelingSalesmanOptimizer("trial 2")
tsp._fit_to_distances(df_distances)
tsp.get_tour_stops_dataframe()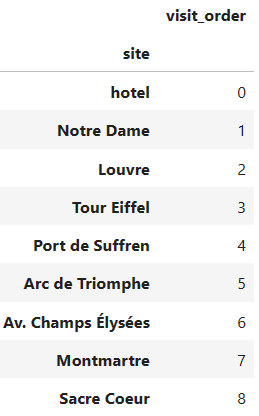Figure 4. Solution (optimal tour) as ranked sites (Image by Author)

The visit_order column indicates we should go from the hotel to Notre Dame, then to the Louvre, and so on, until the last stop before closing the tour, Sacre Coeur. After that, it's trivial that one must return to the hotel. Good, now we have the solution in a format easy to interpret and work with. But the sequence of stops is not all we care about. The value of the objective function is also an important metric to keep track of, as it's the criterion guiding our decisions. For our particular case of the TSP, this means getting the total distance of the optimal tour.

4.2.2 Extracting the optimal objective from the model

In the same manner that we didn’t use the rank variables to extract the sequence of stops because in more complex models their values wouldn’t coincide with the tour stops, we won’t use the objective function directly to obtain the total distance of the tour, even though, here too, both measures are equivalent. In more complex models, the objective function will also incorporate other targets, so this equivalence will no longer hold.

For now, we’ll keep it simple and create a non-public method, _get_tour_total_distance, which clearly indicates the intent. The details of where this distance comes from are hidden, and will depend on the particular targets that more advanced models care about. For now, the details are simple: get the objective value of the solved model.

# class TravelingSalesmanOptimizer(BaseOptimizer):
# def __init__()
# def _create_model()
# def _fit_to_distances()
# def sites()
# def num_sites()
# def initial_site()
# def _get_selected_arcs_from_model()
# def _extract_solution_as_graph()
# def _get_stops_order_list()
# def get_tour_stops_dataframe()

def _get_tour_total_distance(self) -> float:
"""Return the total distance of the optimal tour"""
if self.is_fitted:
# as the objective is an expression for the total distance,
distance_tour = self.model.objective() # we just get its value
return distance_tour

print("Optimizer is not fitted to any data, no optimal objective exists.")
return None

It may look superfluous now, but it’ll serve as a reminder to our future selves that there is a design for grabbing objective values we’d better follow. Let’s check it:

tsp = TravelingSalesmanOptimizer("trial 3")
tsp._fit_to_distances(df_distances)
print(f"Total distance: {tsp._get_tour_total_distance()} m")
# [Out]: Total distance: 14931.0 m

It’s around 14.9 km. As both the optimal tour and its distance are important, let’s make the optimizer store them together whenever the _fit_to_distances method gets called, and only when an optimal solution is found.

4.2.3 Storing the solution in attributes

In the implementation of _fit_to_distances above, we just created a model and solved it, we didn't do any parsing of the solution stored inside the model. Now, we'll modify _fit_to_distances so that when the model solution succeeds, two new attributes are created and made available with the two relevant parts of the solution: the tour_ and the tour_distance_. To make it simple, the tour_ attribute won't return the dataframe we did earlier, it will return the list with ordered stops. The new method _store_solution_from_model takes care of this.

# class TravelingSalesmanOptimizer(BaseOptimizer):
# def __init__()
# def _create_model()
# def sites()
# def num_sites()
# def initial_site()
# def _get_selected_arcs_from_model()
# def _extract_solution_as_graph()
# def _get_stops_order_list()
# def get_tour_stops_dataframe()
# def _get_tour_total_distance()

def _fit_to_distances(self, df_distances: pd.DataFrame):
"""Creates a model of the TSP using the distance matrix
provided in `df_distances`, and then optimizes it.
If the model has an optimal solution, it is extracted, parsed and
stored internally so it can be retrieved.

Parameters
----------
df_distances : pd.DataFrame
Pandas dataframe where the indices and columns are the "cities"
(or any site of interest) of the problem, and the cells of the
dataframe contain the pair-wise distances between the cities, i.e.,
df_distances.at[i, j] contains the distance between i and j.

Returns
-------
self : object
Instance of the optimizer.
"""
model = self._create_model(df_distances)
solution_exists = self._optimize(model)

if solution_exists:
# if a solution wasn't found, the attributes won't exist
self._store_solution_from_model()

return self

#==================== solution handling ====================
def _store_solution_from_model(self) -> None:
"""Extract the optimal solution from the model and create the "fitted
attributes" `tour_` and `tour_distance_`"""
self.tour_ = self._get_stops_order_list()
self.tour_distance_ = self._get_tour_total_distance()

Let’s fit the optimizer again to the distance data and see how easy it is to get the solution now:

tsp = TravelingSalesmanOptimizer("trial 4")._fit_to_distances(df_distances)

print(f"Total distance: {tsp.tour_distance_} m")
print(f"Best tour:\n", tsp.tour_)
# [Out]:
# Total distance: 14931.0 m
# Best tour:
# ['hotel', 'Notre Dame', 'Louvre', 'Tour Eiffel', 'Port de Suffren', 'Arc de Triomphe', 'Av. Champs Élysées', 'Montmartre', 'Sacre Coeur']

Nice. But we can do even better. To further increase the usability of this class, let’s allow the user to solve the problem by only providing the dataframe of sites coordinates. As not everyone will be able to collect a distance matrix for their sites of interest, the class can take care of it and provide an approximate distance matrix. This was done above in section 3.2 with the GeoAnalyzer, here we just put it under the new fit method:

# class TravelingSalesmanOptimizer(BaseOptimizer):
# def __init__()
# def _create_model()
# def _fit_to_distances()
# def sites()
# def num_sites()
# def initial_site()
# def _get_selected_arcs_from_model()
# def _extract_solution_as_graph()
# def _get_stops_order_list()
# def get_tour_stops_dataframe()
# def _get_tour_total_distance()
# def _store_solution_from_model()

def fit(self, df_sites: pd.DataFrame):
"""Creates a model instance of the TSP problem using a
distance matrix derived (see notes) from the coordinates provided
in `df_sites`.

Parameters
----------
df_sites : pd.DataFrame
Dataframe of locations "the salesman" wants to visit, having the
names of the locations in the index and at least one column
named 'latitude' and one column named 'longitude'.

Returns
-------
self : object
Instance of the optimizer.

Notes
-----
The distance matrix used is derived from the coordinates of `df_sites`
using the ellipsoidal distance between any pair of coordinates, as
provided by `geopy.distance.distance`."""
self._validate_data(df_sites)

self._name_index = df_sites.index.name
self._geo_analyzer = GeoAnalyzer()
self._geo_analyzer.add_locations(df_sites)
df_distances = self._geo_analyzer.get_distance_matrix(precision=0)
self._fit_to_distances(df_distances)
return self

def _validate_data(self, df_sites):
"""Raises error if the input dataframe does not have the expected columns"""
if not ('latitude' in df_sites and 'longitude' in df_sites):
raise ValueError("dataframe must have columns 'latitude' and 'longitude'")

And now we have achieved our goal: find the optimal tour from just the sites locations (and not from the distances as before):

tsp = TravelingSalesmanOptimizer("trial 5")
tsp.fit(df_sites)

print(f"Total distance: {tsp.tour_distance_} m")
tsp.tour_
#[Out]:
# Total distance: 14931.0 m
# ['hotel',
# 'Notre Dame',
# 'Louvre',
# 'Tour Eiffel',
# 'Port de Suffren',
# 'Arc de Triomphe',
# 'Av. Champs Élysées',
# 'Montmartre',
# 'Sacre Coeur']

4.3. TravelingSalesmanOptimizer for dummies

Congratulations! We reached the point where the optimizer is very intuitive to use. For mere convenience, I’ll add another method that will be quite helpful later on when we do [sensitivity analysis] and compare the results of different models. The optimizer, as it is now, tells me the optimal visit order in a list, or in a separate dataframe returned by get_tour_stops_dataframe(), but I'd like it to tell me the visit order by transforming the locations dataframe that I give it directly—by returning the same dataframe with a new column having the optimal sequence of stops. The method fit_prescribe will be in charge of this:

# class TravelingSalesmanOptimizer(BaseOptimizer):
# def __init__()
# def _create_model()
# def sites()
# def num_sites()
# def initial_site()
# def _get_selected_arcs_from_model()
# def _extract_solution_as_graph()
# def _get_stops_order_list()
# def get_tour_stops_dataframe()
# def _get_tour_total_distance()
# def _fit_to_distances()
# def _store_solution_from_model()
# def fit()
# def _validate_data()

def fit_prescribe(self, df_sites: pd.DataFrame, sort=True) -> pd.DataFrame:
"""In one line, take in a dataframe of locations and return
a copy of it with a new column specifying the optimal visit order
that minimizes total distance.

Parameters
----------
df_sites : pd.DataFrame
Dataframe with the sites in the index and the geolocation
information in columns (first column latitude, second longitude).

sort : bool (default=True)
Whether to sort the locations by visit order.

Returns
-------
df_sites_ranked : pd.DataFrame
Copy of input dataframe `df_sites` with a new column, 'visit_order',
containing the stop sequence of the optimal tour.

See Also
--------
fit : Solve a TSP from just site locations.

Examples
--------
>>> tsp = TravelingSalesmanOptimizer()
>>> df_sites_tour = tsp.fit_prescribe(df_sites) # solution appended
"""
self.fit(df_sites) # find optimal tour for the sites

if not self.is_fitted: # unlikely to happen, but still
raise Exception("A solution could not be found. "
"Review data or inspect attribute `_results` for details."
)
# join input dataframe with column of solution
df_sites_ranked = df_sites.copy().join(self.get_tour_stops_dataframe())
if sort:
df_sites_ranked.sort_values(by="visit_order", inplace=True)
return df_sites_ranked

Now we can solve any TSP in just one line:

tsp = TravelingSalesmanOptimizer("Paris")

tsp.fit_prescribe(df_sites)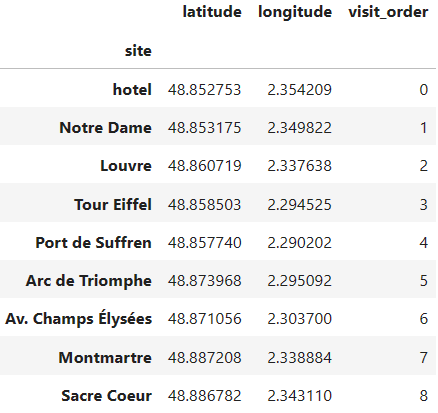Figure 6. Solution (optimal tour) appended to dataframe of sites (Image by Author)

If we’d like to conserve the original order of locations as they were in df_sites, we can do it by specifying sort=False:

tsp.fit_prescribe(df_sites, sort=False)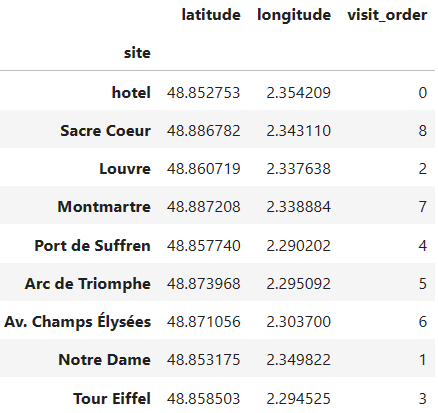Figure 7. Solution appended to dataframe of sites, sites order preserved (Image by Author)

And if we’re curious we can also check the number of variables and constraints the internal model needed to solve our particular instance of the TSP. This will be handy when doing debugging or performance analysis.

tsp.print_model_info()
#[Out]:
# Name: Paris
# - Num variables: 80
# - Num constraints: 74
# - Num objectives: 1

5. Beyond the optimal solution: extracting insights with the optimizer

Before we close this article, I would like to show you some brief examples of how easy it is to use this class, not just to solve TSP problems, but to also answer general questions that usually arise when planning a trip.

For example, suppose you have already come up with a list of sites to visit in one day of your trip to Paris, and you have them in a dataframe called df_sites. You'd like to know only the total length of the optimal tour to traverse them all. You don't have to go to great lengths to know that; this one-liner has you covered:

print(f"Distance: "
f"{TravelingSalesmanOptimizer().fit(df_sites).tour_distance_} m"
)
#[Out]: Distance: 14931.0 m

Now suppose you’re not very sure of your set of sites, and are thinking of trimming it down a little. You are pondering over skipping the visit to Arc de Triomphe, as it is far from the hotel. You may wonder: “How much does the optimal tour change if I don’t go to this site?”. Thanks to the optimizer, getting the answer is straightforward:

site_removed = 'Arc de Triomphe'

df_sites_but_one = df_sites.drop(site_removed, axis=0)
# baseline scenario
tsp_all = TravelingSalesmanOptimizer().fit(df_sites)
# alternative scenario
tsp_all_but_one = TravelingSalesmanOptimizer().fit(df_sites_but_one)

print(
f"Distance tour ({tsp_all.num_sites} sites): {tsp_all.tour_distance_} m",
f"Distance tour without {site_removed}: {tsp_all_but_one.tour_distance_} m",
f"Difference: {tsp_all.tour_distance_ - tsp_all_but_one.tour_distance_} m",
sep="\n"
)
#[Out]:
# Distance tour (9 sites): 14931.0 m
# Distance tour without Arc de Triomphe: 14162.0 m
# Difference: 768 m

With this, you know that you would save around 768 m of walking if you skipped Arc de Triomphe. It’s up to you to decide whether that’s worth it or not.

It’s not just about optimal routes

As another practical example, imagine that you have settled with a list of sites to visit, but haven’t picked a hotel yet. You have several options, and in order to decide better, you would like to know how each choice of hotel impacts the total distance of the tour you’ll make. Then it’s just a matter of fitting another optimizer with a sites dataframe containing the new candidate hotel, and comparing the optimal distance with the optimal distance of using the initial hotel:

# make new locations dataframe with the alternative hotel
df_sites_hotel_2 = df_sites.copy() # sites to visit remain the same
df_sites_hotel_2.loc['hotel'] = (48.828759, 2.329396) # new hotel coordinates

# solve the TSP for each "hotel scenario"
tsp1 = TravelingSalesmanOptimizer("hotel 1").fit(df_sites)
tsp2 = TravelingSalesmanOptimizer("hotel 2").fit(df_sites_hotel_2)

print(f"Distance tour {tsp1.name}: {tsp1.tour_distance_} m")
print(f"Distance tour {tsp2.name}: {tsp2.tour_distance_} m")
print(f"Difference: {tsp2.tour_distance_ - tsp1.tour_distance_} m")
#[Out]:
# Distance tour hotel 1: 14931 m
# Distance tour hotel 2: 17772 m
# Difference: 2841 m

The conclusion is that if we choose “hotel 2”, we will have to walk 2.8 km more than if we chose “hotel 1”, on a tour traversing the same set of sites. All other things being equal, this informs us that “hotel 1” is a better choice than “hotel 2” (given the sites we want to visit).

6. Conclusion (or planning for next sprint)

In this article, we have created two new classes (BaseOptimizer and TravelingSalesmanOptimizer). In future sprints, we'll be using them, extending them, and adding more advanced optimizers to the toolkit, so to do things cleanly, let's move them to a new module, routimizers.py.

Now, one final thing to keep in mind is the scope of this MVP. This first optimizer gives us the answer to the question “in which order should I visit the sites?”, but it doesn’t tell us how to go from one site to the next. That is fine, as that’s the job of GIS applications like Google Maps, not of our humble optimizer.

? Our optimizer solves the tactical problem of telling us the optimal sequence of stops on a tour, not the operational problem of guiding us along that tour. The latter problem is easily solvable by many great GIS applications, like Google Maps.

If you’re happy with the result (the tour), and you’d like to actually implement it in real life, it’s easy: go straight to Google Maps and introduce these sites as stops in the order specified by the optimizer. Hit “go” and there you have your operational answer.

Nevertheless, it still feels like one should be able to visualize the results, not just be content with the numbers that the optimizer puts in a new column; if not for the implementation in real life, at least for a better understanding of the solutions. In sprint 3 we did visualize the solution a bit, even without having the coordinates. Now that we do have the coordinates of the sites, we can do much better and visualize the resulting optimal tours in a more realistic fashion. That is precisely the goal of [our next sprint]: to create nice visuals that enable us to better understand the solutions provided by the optimizer, and in the process, ask and answer more and better questions that allow us to plan better trips.

Stay tuned!

Footnotes

The benefits of this separation will become apparent in future sprints for problems that extend the TSP.Because our class will optimize decisions, not estimate parameters. There’s a subtle difference. Granted, scikit-learn estimators do carry out an optimization under the hood during model training, but the distinction still matters because optimization means different things in Machine Learning and in Operations Research. An estimator uses optimization to estimate the unknown values of the model parameters, while an optimizer uses optimization to find the optimum values of the variables representing decisions we're looking for. Inside estimators, the objective function is a loss function, which measures the extent to which a predicted outcome differs from a true outcome. In optimizers, however, the objective function can be arbitrary, as it is a measure of our desired global state of the world, dependent on our decisions. The key idea is that there's no such thing as "true decisions" that need to be "estimated from data" through optimization techniques. Decisions are prescribed given the data, not estimated from the data.This can happen only due to two reasons: the model is infeasible (the most common), or the model is unbounded (less common, but possible).That’s why, when reading the input coordinates into a dataframe, we read the coordinates of the hotel first.It is a technical requirement that exactly one of the sites does not have an associated rank variable (it doesn’t matter which, but generally the “initial site” is picked). As the hotel was in the index of the first row of df_distances, it was considered the initial site and stored inside the Pyomo model (see attribute tsp.model.initial_site) without an associated rank variable. Remember that the job of the ranks r? is not to indicate the order of visits (that's inherent in ???), but only to prevent the formation of subtours.

Thanks for reading, and see you in the next one! ??

Feel free to follow me, ask me questions, give me feedback, or contact me on LinkedIn.

---

A classy approach to solving Traveling Salesman Problems effectively with Python was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

---

View Entire Post