The Statistical Theory Behind Why Your Instagram Posts Have So Few LikesA handy trick to count uncountable things?—?from Instagram clout, to penguin population and Man City fans in North LondonImage by StockSnap from PixabayWe have all been there …With hopeful eyes, we framed...

The Statistical Theory Behind Why Your Instagram Posts Have So Few Likes

A handy trick to count uncountable things?—?from Instagram clout, to penguin population and Man City fans in North London

Image by StockSnap from Pixabay

We have all been there …

With hopeful eyes, we framed the Christmas spirit through our iPhone 15 lens, capturing the dinner table with an artist’s persistence and a poet’s soul, each photo a festive vignette brimming with friends, the shimmering glaze of the turkey, and the twinkle of ornaments. We meticulously pair every snapshot with an upbeat caption, carefully woven from the threads of our thoughts, hoping each post would jingle all the way through Instagram’s bustling holiday traffic.

And yet, for all the hard work to unveil our holiday spirit to the digital world, we receive a mere 15 likes on our Instagram posts (20 if you count the x-posts on Facebook)

Image by Gerd Altmann from Pixabay

Maybe it is unrealistic to expect a social media uproar if you have a mere 300 Instagram followers, but surely these heartfelt Christmas posts must compel more than 5% of our friends to react, right? The problem is, your total follower count is not the same as your “true audience size”?—?the number of connections that are active and see your posts. You may have many followers, but the majority may not be active, or they may have too dense a follow graph that your posts realistically never reach them.

Then the question is, how can you measure your true social media reach, your Internet clout?

The Lincoln-Peterson index?—?or how to count uncountable things

Let’s say you make an Instagram post on a private account of 300 followers and receive 40 likes. You know your audience is somewhere between 40 and 300. If you have supreme confidence in your ability to craft Instagram posts, you may suppose your reaction rate be 100%, your audience a mere 40 users and it was Instagram who squeeze your reach.

But maybe your photos don’t look too good, or maybe you are not as witty as you think. Maybe you did reach your full 300 followers but you can only get 5% of them to gingerly give you a virtual moral support. There’s no way to know with one post. But if you have two posts, you can get a good idea, even if you don’t know how compelling each individual posts are.

Let’s say your second post has 60 likes and there are 15 mutual likes (people who like both posts). We can naively calculate our true audience size using the good old Set Intersection theory, knowing that it is very conservative estimation, because we potentially neglect a population that doesn’t like either of the Instagram posts.

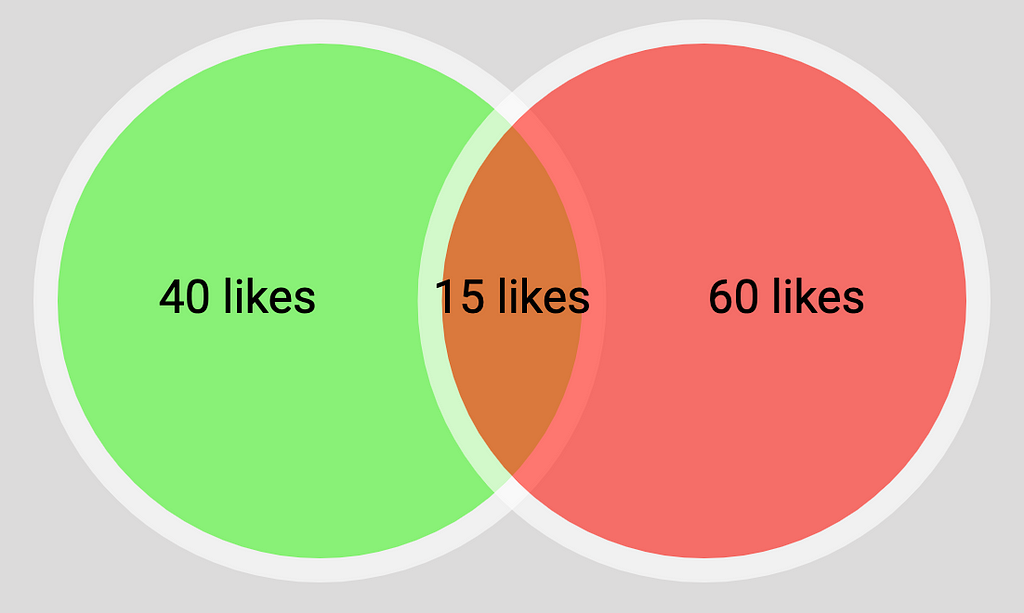Image by author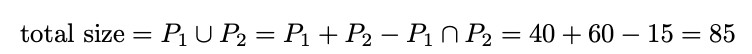

Fortunately, there is a neat method called the Lincoln Index that allows us to estimate the total audience. Let n1, n2 be the number of likes on the first and second post respectively, and m the number of people who like both:

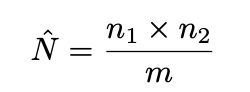
Our estimated reach according to the Lincoln index is 40 x 60/15 = 160. Notice that it is a lot larger than the naive estimate of 85, which exonerates Instagram from squeezing our social clout.

How does it work mathematically??—?or the part where you should feel free to skip

Let us re-frame the problem: we want to choose n2 people to like the second post out of N people, where exactly m out of n2 are among n1 people who like the first post. It should be fairly straightforward that the probability to arrive at such choice is:

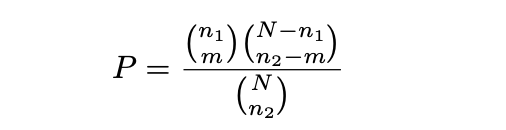
We can use the maximum likelihood method to find an estimate N. For the mathematically inclined, here is an outline of the proof:

The trick is instead of trying to find N that maximizes the likelihood function: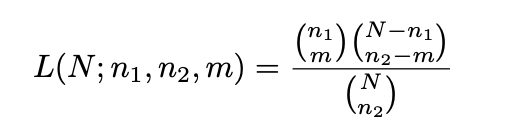we find the largest ? that satisfies the inequality: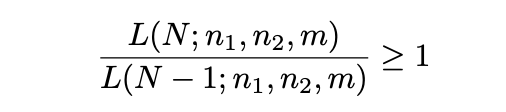it should be obvious, after a bit of arithmetic juggling, that this is equivalent to: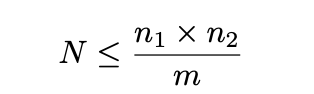And so the estimate N_hat that maximizes the likelihood function has values: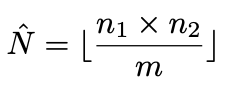

A simulation

I know not everyone is a fan of mathematical proofs so I will try to convince you with a small simulation.

Let’s say we know our social media reach to be 100 and we have 2 Instagram posts with the probability of like p1 and p2, respectively. We can simulate different scenarios of p1 and p2, observe the number of likes on each posts, then reapply the naive Method and the Lincoln methods to see how far each of them are from arriving at the value of 100 (ground truth).

https://medium.com/media/7da82de3d05a94e61bc21d369fdb937a/href

We can see that at different values of p1, p2, the Lincoln estimates remain unbiased (the mean of the 10,000 simulations approximate the true population of 100), while the 95% confidence interval reduces as p1, p2 approximate 1. This makes sense i.e. if we are confident that the like rate of our posts is close to 100%, we should be fairly confident about our audience size estimate. The naive estimate, unfortunately, underestimates our social reach by a lot.

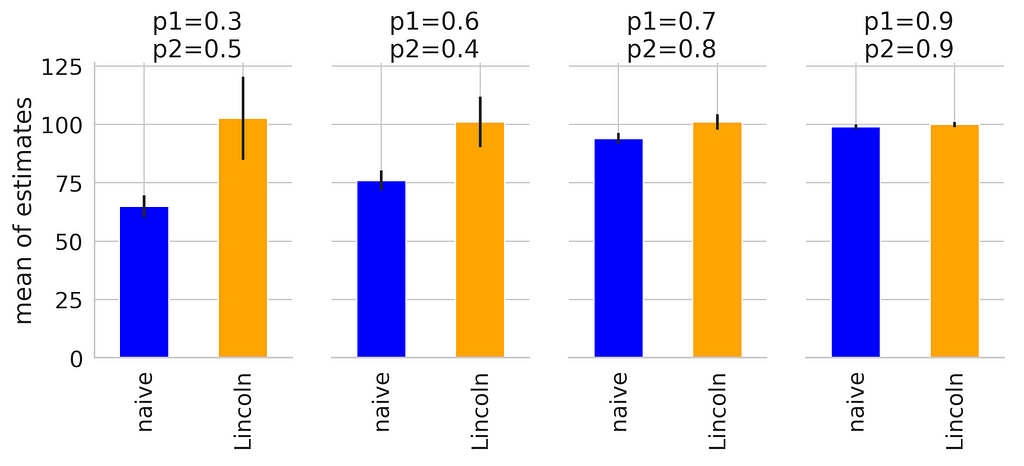Image by author

As usual, all good statistics come with some caveats:

(1) We assume that between each post, the true audience size does not change. This may be true for a casual Instagram user, but probably unrealistic if you are an influencer with an ever increasing fan base.(2) We also assume there are overlapping mutual likes between the two posts. Some of our readers may have found a small cheat in my code:https://medium.com/media/fb8f8f93cf5e6efe90907b92ee941267/href

While the mathematics remain valid, the estimate becomes fairly rough and biased at smaller sample size. Luckily, we have a neat modification, called the Chapman estimate, to address this issue:

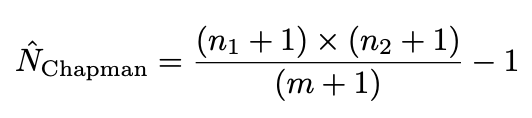
So what is this counting method useful for? This statistical technique— estimating any population size where is impractical to count every individual is very popular in ecology, under a commonly known name mark-recapture method. It is also common to see this method in action in Tech companies, where we want to estimate the amount of bugs in a video game before release, or the amount of policy-violated contents in a social media platform.

I was once challenged in an interview to estimate the number of Man City fans in London. It would have been a fun weekend activity to do some sampling in Trafalgar Square, interviewing people and crunching numbers according to the Lincoln estimate. Although I suspect that the City fans are so few you may actually be able to just count them all!

If you enjoy this article, you may also enjoy my other article about interesting statistical facts and rules of thumbs

Disney Movies were right?—?We are all special, and Statistically soA statistical rule to optimize your life: the Lindy’s EffectRules of Three: Calculating the probability of events that have not yet occurred

For other deep dive analyses:

How Bayesian Statistics convince me to hit the gym?Making big bucks with a data-driven sport betting strategyLove in the time of Pandemic: A Probabilistic approach to Dating

The entire code for this project (simulation and graph) can be found in my Github.

---

The statistical theory behind why your Instagram posts have so few likes was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

---

View Entire Post